Scopeclock
Aus BraLUG-Wiki
(→Die Geschichte mit der ausreichend schnellen Ansteuereinheit) |
(→Download) |
||
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 207: | Zeile 207: | ||
''2.Fazit:'' manchmal ist langsamer doch besser! Die Entscheidung darüber, muss jedes mal neu getroffen werden... | ''2.Fazit:'' manchmal ist langsamer doch besser! Die Entscheidung darüber, muss jedes mal neu getroffen werden... | ||
| + | |||
| + | |||
| + | =Malen nach <strike>Zahlen</strike> ...hmm, Lissajous-Figuren= | ||
| + | [[Bild:Oszi lissajous.jpg|thumb|200px|eine (digital berechnet/erzeugte) Lissajous-Figur]] | ||
| + | Irgendwie sehen die dargestellten Zeichen etwas sperrig aus, wenn sie nur aus Linien konstruiert werden. Da wo eigentlich Rundungen sein sollten (z.B. bei der Zwei, Drei etc.), sind hässliche Kanten und Ecken... | ||
| + | |||
| + | Inspiriert durch die [http://www.sgitheach.org.uk/scope2.html nette Idee] Kreise, Ellipsen, Striche mit Hilfe von [http://de.wikipedia.org/wiki/Lissajous-Figur Lissajous-Figuren] darzustellen, habe ich mich also ans Werk gemacht, dies auch in meiner Scopeclock umzusetzen. Im Gegensatz zur [http://www.sgitheach.org.uk/scope2.html Vorlage], in der das Zeichnen der Lissajous-Firguren hauptsächlich "in Hardware implementiert" ist, baute ich auf die Rechenleistung meines eingesetzten Mikrocontrollers. Die beiden notwendigen Sinusspannungen am X- und Y-Kanal werden rein digital jeweils zur Laufzeit berechnet. | ||
| + | |||
| + | Ausgangspunkt ist dabei eine [http://de.wikipedia.org/wiki/Lookup-Tabelle Lookup-Tabelle] mit 360 Werten einer vollständigen Sinusreihe. Eine 1-Grad-Genauigkeit reicht für diesen Anwendungsfall vollkommen aus. Die Werte in der Tabelle sind bereits mit einem festen Faktor multipliziert, um später mit Ganzzahl-Operationen auszukommen. Theoretisch würde auch eine vorberechnete Sinus-Reihe für 0°...90° reichen, da damit alle anderen Werte berechnet werden könnten. Obwohl diese Berechnungen nicht sonderlich kompliziert sind, gehen diese schon entscheidend in die Gesamtperformance des Algorithmus ein, was sich in einer geringeren Bildwiederholfrequenz bemerkbar macht. Die Menge der zu zeichnen Pixel insgesamt ist dabei entscheidend... ([[Scopeclock#Die_Geschichte_mit_der_ausreichend_schnellen_Ansteuereinheit|siehe auch weiter oben]]). | ||
| + | |||
| + | Die verschiedenen Zeichenelemente (Kreise, Ellipsen, waagerechte/senkrechte/schräge Linien) werden durch die entsprechende Variation der Phasenverschiebung und Amplitudenhöhe beider Sinussignale am X- und Y-Kanal generiert (einfach mal das Grundprinzip von [http://de.wikipedia.org/wiki/Lissajous-Figur Lissajous-Figuren] ansehen und versuchen zu verstehen). Hier mal der Versuch einer Zusammenstellung: | ||
| + | |||
| + | Folgende Gleichungen für das Signal am X- und Y-Kanal liegen zugrunde: | ||
| + | * X = x0+xa*sin(i) | ||
| + | * Y = y0+ya*sin(i+Phasenwinkel) | ||
| + | |||
| + | x0 und y0 bezeichnen den Mittelpunkt der Figur im Koordinatensystem. i ist die Laufvariable von 0° ... 360°. Mit dem Phasenwinkel, xa und ya bestimmt man das letztendliche Aussehen der Figur: | ||
| + | |||
| + | {|cellspacing="0" border="1" | ||
| + | |- style="background-color:#FFF7A5;" | ||
| + | !Element!!Phasenwinkel!!xa!!ya!!Bemerkung | ||
| + | |- | ||
| + | |Kreis/Ellipse | ||
| + | | style="text-align:center;" |90° | ||
| + | |colspan="2"| bestimmt den Durchmesser: | ||
| + | * xa=ya → Kreis mit dem Radius xa bzw. ya | ||
| + | * xa <> ya → Ellipse mit der entsprechenden x-/y-Ausdehnung | ||
| + | | bei Kreissegmenten werden die Kreispunkte an entsprechenden i-Werten (siehe Formel oben) gezeichnen bzw. nicht gezeichnen... | ||
| + | |- | ||
| + | |waagerechte Linie | ||
| + | |style="text-align:center;" |90° | ||
| + | | bestimmt Länge der Linie (vom Mittelpunt x0, y0 gesehen) | ||
| + | | style="text-align:center;" |0 | ||
| + | | es muss nur zwischen i=90° und i=270° gezeichnet werden... | ||
| + | |- | ||
| + | |senkrechte Linie | ||
| + | | style="text-align:center;" |90° | ||
| + | | style="text-align:center;" |0 | ||
| + | | bestimmt Länge der Linie (vom Mittelpunt x0, y0 gesehen) | ||
| + | | es muss nur zwischen i=0° und i=180° gezeichnet werden... | ||
| + | |- | ||
| + | |schräge Linie (nach rechts) | ||
| + | | style="text-align:center;" |0° | ||
| + | |colspan="2"|bestimmen den Anstieg der Linie (also faktisch den Abstand des rechten oberen Endpunktes vom Mittelpunkt x0, y0) | ||
| + | | es muss nur zwischen i=90° und i=270° gezeichnet werden... | ||
| + | |- | ||
| + | |schräge Linie (nach links) | ||
| + | | style="text-align:center;" |180° | ||
| + | |colspan="2"|bestimmen den Anstieg der Linie (also faktisch den Abstand des linken oberen Endpunktes vom Mittelpunkt x0, y0) | ||
| + | | es muss nur zwischen i=90° und i=270° gezeichnet werden... | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | Aus mehreren dieser Grundelemente setzt sich ein Zeichen zusammen (z.B. eine Zwei aus 2 Kreissegmenten und einer waagerechten Linie). Zur Bestimmung der einzelnen Parameter der Zeichenelemente macht sich karriertes Papier ganz gut. Wie in der [http://www.sgitheach.org.uk/scope2.html "Vorlage"], ist auch bei mir die Grundgröße eines Zeichens auf 12x20 festgelegt, da damit recht "ausgewogene" Zeichen konstruierbar sind. Unterschiedliche Zeichengrößen erhält man, wenn jeweils die Parameter x0, y0, xa und ya mit einem entsprechenden Zoomfaktor multipliziert werden. | ||
| + | |||
| + | Meiner Meinung kann sich das Ergebnis dieser "kleinen" Änderung des Bildschirmfonts sehen lassen: | ||
| + | |||
| + | [[Bild:Oszi lissajous analog clock.jpg|240px|analoge Uhr mit Kreisen nach Lissajous...]] | ||
| + | [[Bild:Oszi lissajous font.jpg|240px|Font aus Lissajous-Elementen...]] | ||
| + | [[Bild:Oszi lissajous temperature.jpg|240px|Temperaturanzeige mit "Lissajous-Font"...]] | ||
| + | [[Bild:Oszi lissajous time.jpg|240px|Digitaluhr mit "Lissajous-Font"...]] | ||
=Meine Scopeclock= | =Meine Scopeclock= | ||
| Zeile 274: | Zeile 336: | ||
==Software== | ==Software== | ||
| − | === | + | ===Softwarestruktur Firmware=== |
| + | [[Bild:Scopeclock sw.png|220px|Softwarestruktur Firmware Scopeclock]] | ||
| + | |||
...kommt demnächst! | ...kommt demnächst! | ||
| − | + | ===Download=== | |
| − | === | + | * aktuelle Version unter: [https://github.com/boerge42/scopeclock-stellaris https://github.com/boerge42/scopeclock-stellaris] |
| − | * [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
=Linksammlung= | =Linksammlung= | ||
Aktuelle Version vom 12. April 2020, 09:42 Uhr
Inhaltsverzeichnis |
[Bearbeiten] Vorwort
Der folgende Artikel ist noch nicht vollständig. Er dokumentiert den derzeitigen Stand der Überlegungen und Realisierungen zum Projekt "Scopeclock". Auch in der Endversion wird höchstwahrscheinlich keine wasserdichte Nachbauanleitung zu erwarten sein. Der Text soll lediglich Hilfestellungen zu eigenen Experimenten und Projekten geben.
[Bearbeiten] Warum schon wieder eine Uhr?
Die Darstellung der Uhrzeit ist schon eine interessante Geschichte, mit der man sehr viel Zeit(:-)) verbringen kann. Dass ich mich damit auch ab und zu beschäftige, zeigen einige Uhren-Projekte, die in diesem Wiki zu finden sind. Ich unterscheide dabei zwei Kategorien von Uhrenprojekten:
- Zeitdarstellung in ungewöhnlicher Form
- Zeitdarstellung auf ungewöhnlicher Hardware
Mein letztes Uhren-Projekt, eine Nixie-Uhr, gehört in die zweite Kategorie. Die dabei verwendete Röhrentechnik ist so faszinierend, dass ich den Entschluss gefasst habe, eine weitere Uhr aufzubauen, die ein noch ungewöhnlicheres Ausgabemedium verwendet...
[Bearbeiten] Was ist eine "Scopeclock"?
Herzstück einer Scopeclock ist eine Kathodenstrahlröhre, wie sie z.B. in analogen Oszilloscopen als Anzeigeeinheit eingebaut ist. Prinzipiell wird in einer solchen Röhre ein Elektrodenstrahl erzeugt, welcher in x- und y-Richtung ablenkbar und jeder Zeit abschaltbar (austastbar) ist. Trifft dieser Strahl auf den eingebauten Leuchtschirm, leuchtet die entsprechende Stelle. Erfolgt die Ablenkung und Austastung des Kathodenstrahls in zeitlich geeigneter Art und Weise, können damit Linien, Punkte etc. erzeugt werden. Mit einem Oszilloskop wird damit z.B. der zeitliche verlauf einer Spannung dargestellt. ...und bei einer Scopeclock werden aus den Linien und Punkten Ziffern/Zeichen, Uhrenziffernblätter und Uhrzeiger zusammengesetzt...!
Sucht man bei der Suchmaschine seiner Wahl nach entsprechenden Bildern (Suchbegriff: Scopeclock), erahnt man, wie eine solche Uhr aussehen könnte. Die Bilder zu meinem Scopeclock-Simulator deuten ähnliche Darstellungsformen für Datum/Uhrzeit an.
[Bearbeiten] Scopeclock-Simulator
Komischerweise fragt man sich als Softwareentwickler (fast) immer zuerst, wie müßte ungefähr das Programm, der Algorithmus aussehen, wenn man dieses und jenes Ergebnis haben möchte. Hat man ein wenig Zeit, schreibt man halt einen Simulator, um ein wenig zu experimentieren...
Im Fall der Scopeclock kommt allerdings noch ein weiterer Aspekt hinzu: für die Ansteuerung der Anzeigeröhre soll ein Mikrocontroller (Hersteller/Typ steht zu diesem Zeitpunkt noch nicht fest) eingesetzt werden. Wegen des begrenzten Programmspeichers und Geschwindigkeit müssen Algorithmen gefunden werden, die schnell und platzsparend arbeiten. Gerade bei der Darstellung des analogen Ziffernblattes (es handelt sich bekanntlich um einen Kreis) verbietet es sich also Rechenoperationen mit Komma-Zahlen (welcher konkrete Typ auch immer) zu verwenden. Damit sind auch die originären Winkelfunktionen tabu! Weiterhin musste ein einfache Möglichkeit her, mit der man Zahlen (und andere Zeichen) platzsparend und skalierbar erzeugen kann.
Ergebnis ist ein Scopeclock-Simulator, der in Tcl/Tk geschrieben wurde. Innerhalb der Software wurden die beiden vorgesehenen Anzeigemodi (eine analoge und eine digitale Darstellungsform) umgesetzt. Sämtliche verwendete Algorithmen kommen mit 16-Bit-Integer aus. Eine Portierung der entscheidenen Tcl-Routinen in C sollte problemlos möglich sein. Speziell wurde folgendes getestet/umgesetzt:
- Definition der Zeichen als Punktfolgen, die mit Geraden untereinander verbunden werden und skalierbar sind
- Zeichnen von Linien mit Hilfe des Bresenham-Algorithmus (Kreise zeichnen auch, wird aber wahrscheinlich später nicht benötigt...)
- Berechnung von Winkelfunktionen mit Hilfe einer Lookup-Tabelle und temporärer Skalierung auf verlustminimierter Integer-Operationen
Im Simulator wird nicht die eigentliche Ansteuerung der Oszillographenröhre nachgestellt. Es wird von der Annahme ausgegangen, dass es einen zweidimensionalen Bildspeicher (128x128x1 Bit, also in 2048 Byte RAM abbildbar) gibt, in dem das anzuzeigende Bild statisch aufgebaut wird. Dieser Bildspeicher wird später zyklisch fortlaufend (Stichwort: Timer-Interrupt) von einer weiteren Routine ausgelesen werden, die wiederum die Hardware (insbesondere Digital-/Analog-Wandler) zur Röhrenansteuerung mit Daten versorgt.
[Bearbeiten] Ein paar vorbereitende Software-Experimente
Irgendwo muss man anfangen! Mit 600V "in Hardware" wollte ich nicht beginnen. Also musste ein analoges Oszilloscope her, welches in X-/Y- sowie Z-Richtung ("Strahl-Helligkeit") jeweils seperat ansteuerbar ist. Ein gutes altes EO-174A aus DDR-Zeiten scheint genau das Richtige für diese prinzipielle Experimente zu sein und konnte im Bekanntenkreis aufgetrieben werden... Später kam dann ein EO 213 zum Einsatz.
[Bearbeiten] Einfach mal etwas auf dem Oszi ausgeben...
Einfachste Geschichte ist, wenn man aus zwei Bits vier Punkte ({L, L}, {H, L}, {H, H}, {L, H}) aus den resultierenden Spannungspegeln für Low/Height generiert und an den entsprechenden X-/Y-Eingängen des Oszi ausgibt. Für ein Stellaris Launchpad würde das dazu notwendige Programm wie folgt aussehen:
#include "inc/hw_memmap.h"
#include "inc/hw_types.h"
#include "driverlib/gpio.h"
#include "driverlib/sysctl.h"
#define XY_PORT_BASE GPIO_PORTB_BASE
#define XY_SYSCTL_PERIPH SYSCTL_PERIPH_GPIOB
#define PIN_XOUT GPIO_PIN_0
#define PIN_YOUT GPIO_PIN_1
#define DELAY 100
int main()
{
SysCtlPeripheralEnable(XY_SYSCTL_PERIPH);
GPIOPinTypeGPIOOutput(XY_PORT_BASE, PIN_XOUT|PIN_YOUT);
while (1) {
GPIOPinWrite(XY_PORT_BASE, PIN_XOUT|PIN_YOUT, 0);
SysCtlDelay(DELAY);
GPIOPinWrite(XY_PORT_BASE, PIN_XOUT|PIN_YOUT, PIN_XOUT);
SysCtlDelay(DELAY);
GPIOPinWrite(XY_PORT_BASE, PIN_XOUT|PIN_YOUT, PIN_XOUT|PIN_YOUT);
SysCtlDelay(DELAY);
GPIOPinWrite(XY_PORT_BASE, PIN_XOUT|PIN_YOUT, PIN_YOUT);
SysCtlDelay(DELAY);
}
}
[Bearbeiten] Striche zeichnen
Neben dem Stellaris Launchpad kam bei diesem Versuch ein Digital/Analog-Wandler (DAC) vom Typ TLC7528 zum Einsatz. Dieser DAC besitzt 2 Kanäle mit jeweils 8-Bit Breite. Die Kanalwahl erfolgt über ein entsprechendes Eingangs-Pin und die umzusetzenden Digitalwerte werden parallel an den DAC weitergegeben. Das Datenblatt des TLC7528 sollte genügend Aufklärung geben. Für diesen Versuch wurde der DAC im "Voltage Mode" betrieben. Mit den beiden DAC-Kanälen werden die Spannungswerte für die x- und y-Auslenkung am Oszi generiert. Der Rest sollte aus dem Quelltext hervorgehen:
#include <stdint.h>
#include "inc/hw_memmap.h"
#include "inc/hw_types.h"
#include "driverlib/gpio.h"
#include "driverlib/sysctl.h"
// Daten-Port DAC (TLC7528)
#define DATA_OUT GPIO_PIN_0|GPIO_PIN_1|GPIO_PIN_2|GPIO_PIN_3|GPIO_PIN_4|GPIO_PIN_5|GPIO_PIN_6|GPIO_PIN_7
#define DATA_PORT_BASE GPIO_PORTB_BASE
#define DATA_SYSCTL_PERIPH SYSCTL_PERIPH_GPIOB
// Steuerleitungen DAC (TLC7528)
#define DAC_CTL_PORT_BASE GPIO_PORTE_BASE
#define DAC_CTL_SYSCTL_PERIPH SYSCTL_PERIPH_GPIOE
#define DAC_AB GPIO_PIN_1
#define DAC_WR GPIO_PIN_2
#define DAC_CS GPIO_PIN_3
#define DAC_CH_A 0
#define DAC_CH_B DAC_AB
#define MAX_X 255
#define MAX_Y 255
#define DT_X 255/MAX_X
#define DT_Y 255/MAX_Y
// *********************************
void xy_set(uint8_t x, uint8_t y)
{
// x
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_AB, 0);
GPIOPinWrite(DATA_PORT_BASE, DATA_OUT, x*DT_X);
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_WR, 0);
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_WR, DAC_WR);
// y
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_AB, DAC_AB);
GPIOPinWrite(DATA_PORT_BASE, DATA_OUT, y*DT_Y);
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_WR, 0);
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_WR, DAC_WR);
// Punkt kurz halten
SysCtlDelay(20);
}
// *********************************
int abs(int value)
{
return value<0 ? -value : value;
}
// *********************************
// http://de.wikipedia.org/wiki/Bresenham-Algorithmus
//
void line(int x0, int y0, int x1, int y1)
{
int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1;
int dy = -abs(y1-y0), sy = y0<y1 ? 1 : -1;
int err = dx+dy, e2; /* error value e_xy */
for(;;){ /* loop */
xy_set(x0,y0);
if (x0==x1 && y0==y1) break;
e2 = 2*err;
if (e2 > dy) { err += dy; x0 += sx; } /* e_xy+e_x > 0 */
if (e2 < dx) { err += dx; y0 += sy; } /* e_xy+e_y < 0 */
}
}
// *********************************
// *********************************
// *********************************
int main()
{
// Systemtakt 80MHz...
SysCtlClockSet(SYSCTL_SYSDIV_2_5 | SYSCTL_USE_PLL | SYSCTL_OSC_MAIN | SYSCTL_XTAL_16MHZ);
// ...DAC-DATA-Port
SysCtlPeripheralEnable(DATA_SYSCTL_PERIPH);
GPIOPinTypeGPIOOutput(DATA_PORT_BASE, DATA_OUT);
// ...DAC-Control-Pins
SysCtlPeripheralEnable(DAC_CTL_SYSCTL_PERIPH);
GPIOPinTypeGPIOOutput(DAC_CTL_PORT_BASE, DAC_AB|DAC_WR|DAC_CS);
// ... CS=Low; WR=Hight
GPIOPinWrite(DAC_CTL_PORT_BASE, DAC_WR|DAC_CS, DAC_WR);
while (1) {
line (0, 0, MAX_X, 0);
line (MAX_X, 0, MAX_X, MAX_Y);
line (MAX_X, MAX_Y, 0, MAX_Y);
line (0, MAX_Y, 0, 0);
line (0, 0, MAX_X, MAX_Y);
line (0, MAX_Y, MAX_X, 0);
}
}
Damit sind eigentlich alle Voraussetzungen vorhanden, die Software für die Scopeclock zu schreiben, denn wenn man Punkte und Linien zeichnen kann, sollte alles andere kein Problem darstellen. Der Rest ist dann nur noch Fleißarbeit, wie man auf den folgenden Bildern sieht:
[Bearbeiten] Die Geschichte mit der ausreichend schnellen Ansteuereinheit
Kluge Leute haben irgendwann mal ermittelt/festgestellt, dass das menschliche Auge recht träge ist. Ab einer Bildwiederholfrequenz von ca. 50Hz werden die einzelnen Bilder nicht mehr als flimmernd empfunden. OK, dass scheint also die magische Zahl zu sein!
D.h. aber auch, die Ansteuereinheit der geplanten Scopeclock, vornehmlich der verwendete Mikrocontroller (MCU), muss schnell genug sein, die Bilddaten 50 Mal in der Sekunde zu berechnen und an den angeschlossenen Digital-Analog-Wandler weiterzugebenen. Eine Milchmädchenrechnung würde ungefähr so aussehen:
- ein kompletes Bild muss in 1/50Hz=20ms fertig berechnet und ausgegeben sein → hört sich noch nicht ungemein schnell an...
- wenn ein Bild aus vielleicht 2000 Bildpunkten besteht, muss einer von diesen Punkten, im Mittel, in ca. 20ms/2000=0,01ms berechnet sein → jetzt wird es wohl doch spannend...
- ...denn 1/0,00001s=100kHz!
Was heißt das? Eine mit 20MHz getaktete MCU hat also im Mittel(!) 200 Taktzyklen Zeit einen Bildpunkt zu berechnen. Schon recht sportlich, denn:
- dauert jeder Maschinenbefehl wirklich nur einen Taktzyklus?
- den nächsten Punkt in einem Kreis oder auf einer gedachten Linie berechnen mit 200 Maschinenbefehlen? OK, vielleicht in Assembler, aber wer will das schon wirklich? (Anmerkung: Wer jetzt meint, ein einmal vorberechnetes Bild würde ja auch gehen, ist auf dem Holzweg! Dieses Bild muss ja auch irgendwo eine festgelegte Größe haben, z.B. 128x128=16384 Bildpunkte, ...upps Faktor 8 im Vergleich zu 2000 Bildpunkten → 200/8... nur noch 25 MCU-Takte pro Bildpunkt berechnen/ausgeben/etc. ...!)
- "nebenbei" müssen auch noch ein paar andere Dinge erledigt werden (z.B. Datum/Uhrzeit hochzählen, Bedienung etc.)
- ...und, kein Mensch plant gleich von Anfang an, hart an den Grenzen!
Aus diesem Grund wurde mit dem LM4F120H5QR (MCU-Takt 80MHz) auf einem Stellaris Launchpad eine ausreichend schnelle MCU für das Projekt gefunden. Das diese Wahl nicht unbedingt falsch war, bestätigen die real ermittelten Werte für die erreichten Bildwiederholfrequenz in den verschiedenen Anzeigearten (...und ja, jeder Bildpunkt wird dabei in jedem auszugebenden Bild entsprechend neu berechnet!) → siehe auch Diagramm zu diesem Absatz!
Und selbst diese MCU würde nicht schnell genug sein ein z.B. 128x128 Bildpunkte großes Bild einfach statisch auszugeben (Berechnung des Bildinhaltes noch nicht mal einberechnet), denn ca. 32Hz Bildwiederholfrequenz sind einfach zu wenig, ...es flimmert!
Anmerkung vom 25.11.2013:
Am Wochenende habe ich eine Funktion geschrieben, die XBM-Bilder auf dem Scope darstellen sollte. Die erste (unbedarfte) Implementierung war, trotz schneller MCU, zu langsam. Es wurde eine Bildwiederholfrequenz von ca. 43Hz (bei 6175 darzustellenden Bildpunkten) erreicht, was zu einem deutlichen Flimmern führte. Nach einigen Experimenten stellte sich heraus, dass vor allem eine Modulo-Operation, welche nach dem Lesen jedes Bytes der Bilddaten ausgeführt wurde, einen Hauptanteil an der langsamen Berechnung hatte. Nach deren Eliminierung und einigen weiteren gezielten Optimierungen (z.B. direkte Pointerinkrementierung statt Hochzählen von Feldindizes, explizietes Maskieren eines Bytes mit 8 entsprechenden Statements statt in einer kürzeren/eleganten for-Schleife), wird jetzt das gleiche XBM-Bild mit einer Bildwiederholfrequenz von ca. 76Hz, und damit flimmerfrei, dargestellt.
"Zwischenfazit:" trotz vermeindlich schneller MCU, lohnt es sich, an entscheidenen Stellen auch mal etwas länger über die Implementierung von Algorithmen nachzudenken und zu experimentieren, um schnelleren Code zu erhalten. Oft stellt sich auch heraus, dass kompakter/eleganter Code nicht der effektivere ist. Nicht immer sollte man einen "Schönheitspreis" gewinnen wollen...!
Schizophrener Weise kann aber die Verarbeitungsgeschwindigkeit der MCU, bzw. des verwendeten Algorithmus, auch zu hoch sein, um das gewünschte Ergebnis zu erhalten: In einem weiteren Experiment sollte ein Kreis mit Hilfe des entsprechenden "Bresenham-Algorithmus" auf dem Scope ausgegeben werden. Das Ergebnis sieht so gar nicht nach einem Kreis aus! Erst nach etwas Überlegung erkennt man das Problem. Schaut man sich den Algorithmus etwas genauer an, stellt man fest, dass, wegen der Symmetrie des Kreises in acht gedachten Oktanten, nach jedem Berechnungsschritt acht Kreispunkte quasi gleichzeitig ausgegeben werden. Dieses fast gleichzeitige Ausgeben ist aber sehr viel schneller, als die Berechnung des ersten der acht Punkte und die Positionierungzeit des Kathodenstrahls zwischen den daraus resultierenden Punkten in den acht Quadranten. Man sieht also eigentlich nur noch die Positionierungsbewegung des Strahls. Erst wenn man die Ausgabe drosselt und jeden ausgegebenen Kreispunkt länger "hält", erkennt man, dass es wirklich ein Kreis ist.
2.Fazit: manchmal ist langsamer doch besser! Die Entscheidung darüber, muss jedes mal neu getroffen werden...
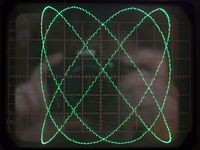
[Bearbeiten] Malen nach Zahlen ...hmm, Lissajous-Figuren
Irgendwie sehen die dargestellten Zeichen etwas sperrig aus, wenn sie nur aus Linien konstruiert werden. Da wo eigentlich Rundungen sein sollten (z.B. bei der Zwei, Drei etc.), sind hässliche Kanten und Ecken...
Inspiriert durch die nette Idee Kreise, Ellipsen, Striche mit Hilfe von Lissajous-Figuren darzustellen, habe ich mich also ans Werk gemacht, dies auch in meiner Scopeclock umzusetzen. Im Gegensatz zur Vorlage, in der das Zeichnen der Lissajous-Firguren hauptsächlich "in Hardware implementiert" ist, baute ich auf die Rechenleistung meines eingesetzten Mikrocontrollers. Die beiden notwendigen Sinusspannungen am X- und Y-Kanal werden rein digital jeweils zur Laufzeit berechnet.
Ausgangspunkt ist dabei eine Lookup-Tabelle mit 360 Werten einer vollständigen Sinusreihe. Eine 1-Grad-Genauigkeit reicht für diesen Anwendungsfall vollkommen aus. Die Werte in der Tabelle sind bereits mit einem festen Faktor multipliziert, um später mit Ganzzahl-Operationen auszukommen. Theoretisch würde auch eine vorberechnete Sinus-Reihe für 0°...90° reichen, da damit alle anderen Werte berechnet werden könnten. Obwohl diese Berechnungen nicht sonderlich kompliziert sind, gehen diese schon entscheidend in die Gesamtperformance des Algorithmus ein, was sich in einer geringeren Bildwiederholfrequenz bemerkbar macht. Die Menge der zu zeichnen Pixel insgesamt ist dabei entscheidend... (siehe auch weiter oben).
Die verschiedenen Zeichenelemente (Kreise, Ellipsen, waagerechte/senkrechte/schräge Linien) werden durch die entsprechende Variation der Phasenverschiebung und Amplitudenhöhe beider Sinussignale am X- und Y-Kanal generiert (einfach mal das Grundprinzip von Lissajous-Figuren ansehen und versuchen zu verstehen). Hier mal der Versuch einer Zusammenstellung:
Folgende Gleichungen für das Signal am X- und Y-Kanal liegen zugrunde:
- X = x0+xa*sin(i)
- Y = y0+ya*sin(i+Phasenwinkel)
x0 und y0 bezeichnen den Mittelpunkt der Figur im Koordinatensystem. i ist die Laufvariable von 0° ... 360°. Mit dem Phasenwinkel, xa und ya bestimmt man das letztendliche Aussehen der Figur:
| Element | Phasenwinkel | xa | ya | Bemerkung |
|---|---|---|---|---|
| Kreis/Ellipse | 90° | bestimmt den Durchmesser:
|
bei Kreissegmenten werden die Kreispunkte an entsprechenden i-Werten (siehe Formel oben) gezeichnen bzw. nicht gezeichnen... | |
| waagerechte Linie | 90° | bestimmt Länge der Linie (vom Mittelpunt x0, y0 gesehen) | 0 | es muss nur zwischen i=90° und i=270° gezeichnet werden... |
| senkrechte Linie | 90° | 0 | bestimmt Länge der Linie (vom Mittelpunt x0, y0 gesehen) | es muss nur zwischen i=0° und i=180° gezeichnet werden... |
| schräge Linie (nach rechts) | 0° | bestimmen den Anstieg der Linie (also faktisch den Abstand des rechten oberen Endpunktes vom Mittelpunkt x0, y0) | es muss nur zwischen i=90° und i=270° gezeichnet werden... | |
| schräge Linie (nach links) | 180° | bestimmen den Anstieg der Linie (also faktisch den Abstand des linken oberen Endpunktes vom Mittelpunkt x0, y0) | es muss nur zwischen i=90° und i=270° gezeichnet werden... | |
Aus mehreren dieser Grundelemente setzt sich ein Zeichen zusammen (z.B. eine Zwei aus 2 Kreissegmenten und einer waagerechten Linie). Zur Bestimmung der einzelnen Parameter der Zeichenelemente macht sich karriertes Papier ganz gut. Wie in der "Vorlage", ist auch bei mir die Grundgröße eines Zeichens auf 12x20 festgelegt, da damit recht "ausgewogene" Zeichen konstruierbar sind. Unterschiedliche Zeichengrößen erhält man, wenn jeweils die Parameter x0, y0, xa und ya mit einem entsprechenden Zoomfaktor multipliziert werden.
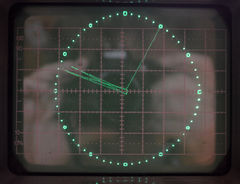
Meiner Meinung kann sich das Ergebnis dieser "kleinen" Änderung des Bildschirmfonts sehen lassen:
[Bearbeiten] Meine Scopeclock
[Bearbeiten] Hardware
[Bearbeiten] Kathodenstrahlröhre
Die Anschaffung der notwendigen Kathodenstrahlröhre war die erste vollendete Tatsache (also die erste finanzielle Ausgabe) zu diesem Projekt. Meine Wahl fiel auf ein Exemplar mit "niedrigen" Betriebsspannungen, eine DG7-32 von Philips. Da solche Röhren nicht mehr im regulären Handel erhältlich sind, wurde sie über ein bekanntes Internet-Auktionshaus beschafft. Einige spezialisierte Privathändler haben ebenfalls solche Bauteile im Sortiment (z.B. "Frag' Jan zuerst").
Datenblatt der Kathodenstrahlröhre DG7-32
...achso, "Niedrige Betriebsspannungen" bedeuten immer noch ca. 600V für die Gitterspannung...;-) Bei anderen Röhrentypen geht das auch schon mal weit über 1000V!
[Bearbeiten] Netzteil
Heute kam mein bestellter Ringkerntrafo (und die Röhrenfassung) an. Diese beiden Teile habe ich bei Jan Wüsten geordert.
Das heißt also, dass es jetzt langsam mit dem Aufbau der Hardware losgehen kann, wenn der Rest der notwendigen Bauteile von meinem Lieblings-Elektronik-Versender angekommen sind...
Als Vorlage für Netzteil wird die entsprechend angepasste Schaltung aus dem Projekt von Sascha Ittner (Seite 2 bis 4) verwendet.
[Bearbeiten] Ansteuereinheit
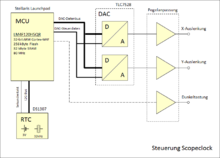
Ein (vereinfachtes) Blockschaltbild könnte ungefähr so aussehen:
Folgende Hauptkomponenten sind zu erkennen:
- Mikrocontroller (MCU)
- hier ein Stellaris Launchpad
- holt initial Datum/Uhrzeit von der RTC und zählt diese in der Folge weiter
- generiert die anzuzeigenden Bilddaten, berechnet daraus die resultierenden Eingangsdaten für die beiden DAC-Kanäle (X-/Y-Auslenkung) und leitet diese entsprechend dorthin weiter
- gewährleistet die Bedienung über 2 Taster (derzeit Umschalten der Anzeigemodi und Einstellen von Datum/Uhrzeit)
- Real Time Clock (RTC)
- ein DS1307 mit einer 3V-Pufferbatterie und einem 32kHz-Uhrenquarz
- mit der MCU via I²C-Bus verbunden
- speichert und zählt die Zeit weiter, wenn die Gesamtbaugruppe ausgeschaltet ist
- generiert den (genauen) Sekundentakt für die MCU
- Digital-Analog-Wandler (DAC)
- verwendet wird ein TLC7528 (2 Kanäle, 8-bit-DAC); im "Voltage Mode" (siehe Datenblatt) betrieben
- erzeugt die Spannungen, aus der dann die X- und Y-Auslenkung des Kathodenstrahls resultieren
- Pegelanpassung
- wird im jetzigen Stadium (Ausgabe auf einem Oszilloskop) noch nicht benötigt, wird aber später zur Verstärkung der DAC-Ausgangsspannungen an die Eingangsparameter der Kathodenstrahlröhre benötigt...
Hier ein paar Bilder vom derzeitigen Aufbau der Ansteuereinheit:
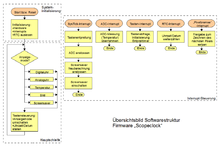
[Bearbeiten] Software
[Bearbeiten] Softwarestruktur Firmware
...kommt demnächst!
[Bearbeiten] Download
- aktuelle Version unter: https://github.com/boerge42/scopeclock-stellaris
[Bearbeiten] Linksammlung
- Beschaffung von Röhren, Fassungen, Trafos:
- Beispielprojekte:
- http://www.jogis-roehrenbude.de/Leserbriefe/Scope-Clock/Scope-Clock.htm
- http://www.jogis-roehrenbude.de/Leserbriefe/Erhards_Scope-Clock/HS_ScopeClock.htm
- http://www.webx.dk/oz2cpu/clock-scope/scope.htm
- http://dutchtronix.com/ScopeClock.htm
- http://www.electronixandmore.com/project/scopeclock/index.html
- http://www.mikrocontroller.net/topic/97963
- http://www.derivedlogic.com/Scope%20Clock/scopeclock.html
- http://www.microsyl.com/index.php/2010/03/28/scope-clock/
- http://www.cathodecorner.com/sc200c.html
- http://www.sgitheach.org.uk/scope2.html
[Bearbeiten] Kontakt
Fragen und Anregungen können an Uwe gerichtet werden...